deep learning 人工智能机器学习 tensorflow 深度学习神经网络

机器学习

Publish Date: 2025-02-06

Word Count: 7k

Read Times: 25 Min

Read Count:

吴恩达机器学习 Course2 week2 神经网络的训练

1 Tensorflow神经网络的编译和训练

1-1 Tensorflow的实现

# compile()函数所有的可选选项及其示例
model.compile(loss=tf.keras.losses.BinaryCrossentropy(),
              optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
              metrics='accuracy'
)

编译compile()：输入参数有“损失函数loss”、“优化器optimizer”、“评估指标metrics”。主要考虑前两项。
- “损失函数loss”：决定了神经网络的代价函数。在“训练”的某次迭代结束后，利用输出层的输出结果与真实目标值之间的差异计算神经网络的代价。进而可以通过反向传播更新参数。
- “优化器optimizer”：则是“梯度下降法”的升级版，可以选择性能更强大、收敛速度更快的迭代算法。
- “评估指标metrics”：和“训练”本身没有关系，和损失函数没有关系。只是在“训练”的单次迭代结束后，衡量一下所有训练集的推理结果与真实值之间的差异。loss也有此作用，但是不直观；metrics可以选择更加直观的指标，比如metrics=’accuracy’可以计算“推理正确的训练样本”的百分比。
```
# compile()函数所有的可选选项及其示例
model.compile(loss=tf.keras.losses.BinaryCrossentropy(),
              optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
              metrics='accuracy'
)
```

训练fit()：有非常多的指标可以设置，但我们现在仅关心“数据集”、“迭代次数epchos”即可(下面代码示例的前三项)。注意每次迭代都会使用到所有的训练集样本，若样本太多，程序会自动将数据分批。并且，运行fit()函数后，会自动打印输出训练过程。

# fit()函数所有的可选选项及其示例
model.fit(
    x=None,                # 输入数据
    y=None,                # 标签
    epochs=1,              # 训练轮数
    batch_size=None,       # 指定进行梯度下降时每个批次包含的样本数
    verbose=1,             # 控制训练过程中的日志输出，0：不输出日志，1：输出进度条记录，2：每个epoch输出一行记录
    callbacks=None,        # 在训练过程中调用的回调函数列表
    validation_split=0.0,  # 用于验证的训练数据的比例
    validation_data=None,  # 用于验证的数据，可以是输入数据和标签的元组
    shuffle=True,          # 是否在每个epoch之前随机打乱输入数据
    class_weight=None,     # 类别权重
    sample_weight=None,    # 样本权重
    initial_epoch=0,       # 开始训练的epoch值
    steps_per_epoch=None,  # 每个epoch包含的步数，当为None时，将自动计算
    validation_steps=None, # 在每个epoch结束时执行验证的步数，当为None时，将自动计算
    validation_batch_size=None,  # 用于验证的批次大小
    validation_freq=1,     # 仅在`validation_data` 的某些训练轮上进行验证
    max_queue_size=10,     # 生成器队列的最大尺寸
    workers=1,             # 使用的生成器工作进程数
    use_multiprocessing=False,  # 是否使用多进程生成器
    **kwargs
)
# 运行fit()函数后，会自动打印输出训练过程，下面为单次迭代的输出示例
Epoch 1/40
157/157 [==============================] - 1s 1ms/step - loss: 1.5179 - accuracy: 0.5406

主要参数(by deepseek)

参数	类型/默认值	说明
`x`	输入数据	训练数据的特征（可以是 NumPy 数组、TensorFlow Dataset、生成器等）。
`y`	标签数据	训练数据的标签（与 `x` 对应）。如果 `x` 是 Dataset，可省略。
`epochs`	int, 默认 1	训练的总轮次（完整遍历训练数据的次数）。
`batch_size`	int, 默认 32	每个批次的样本数。如果数据是 Dataset 或生成器，可忽略。
`verbose`	0/1/2, 默认 1	日志显示模式： - `0`: 静默模式 - `1`: 进度条 - `2`: 每轮一行输出。
`callbacks`	list, 默认 `[]`	回调函数列表（如 `EarlyStopping`, `ModelCheckpoint` 等）。
`validation_split`	float (0~1), 默认 0	从训练数据中划分一部分作为验证数据的比例（不能与 `validation_data` 同时使用）。
`validation_data`	数据集或元组	验证数据（可以是 `(x_val, y_val)` 或 Dataset）。
`shuffle`	bool, 默认 True	是否在每个 epoch 前打乱训练数据顺序（对 Dataset 无效，需提前定义）。
`class_weight`	dict, 默认 None	类别权重（用于不平衡分类问题，如 `{0: 1.0, 1: 0.5}`）。
`sample_weight`	array-like, 默认 None	样本权重（调整每个样本在损失函数中的权重）。
`initial_epoch`	int, 默认 0	从指定 epoch 开始训练（用于恢复训练）。
`steps_per_epoch`	int, 默认 None	每个 epoch 的批次数量。若为 None，自动根据数据量计算。
`validation_steps`	int, 默认 None	验证集的批次数量（仅当 `validation_data` 是生成器时需指定）。
`validation_batch_size`	int, 默认 None	验证集的批次大小。
`validation_freq`	int/list, 默认 1	验证频率（如 `2` 表示每 2 个 epoch 验证一次）。
`max_queue_size`	int, 默认 10	生成器队列的最大大小（多进程数据加载时使用）。
`workers`	int, 默认 1	生成器数据加载的进程数。
`use_multiprocessing`	bool, 默认 False	是否使用多进程加载生成器数据。

官方文档：https://www.tensorflow.org/api_docs/python/tf/keras/Model#fit

熟悉了上面的选项之后，回到简化的“手写数字识别”问题，其训练代码如下，主要看“编译model.compile()”和“训练model.fit()”：

定义神经网络。定义神经网络的层数、每层神经元数量、激活函数。和之前相同。

编译神经网络。关键在于确定损失函数，由于是二元分类问题所以选取了“二元交叉熵损失函数”。

训练神经网络。X,Y为训练集、epochs为迭代次数，也就是“梯度下降法”的迭代次数，每次迭代都会使用全部训练集的数据。

1-2 模型训练细节

损失函数和代价函数的公式：

第一步创建model:

第二步：决定指定用什么损失函数、成本函数来训练神经网络：

对于手写数字分类，图像要么是0，要么是1，损失函数实际与逻辑回归损失函数相同，在统计学上被称作交叉熵损失函数（binary cross entropy），所以“complie” 所配置的损失函数是loss=BinaryCrossentropy()，而“二元”只是强调输出为二元分类，所以称之为“二元交叉熵损失函数”

在代码实现中，Keras库最初是独立的数学函数库，后来被TensorFlow收录，所以TensorFlow使用Keras库来定义损失函数。这也是最初的代码中，从keras导入损失函数的原因。

当然上述是对“分类问题”的代码，如果想编译“回归问题”，可以采用下面的代码(注意修改损失函数):

# 回归问题中，使用“平方差损失函数”编译模型
from tensorflow.keras.losses import MeanSquareError
model.compile(loss = MeanSquareError())

$$
\text{Loss Function: } \quad L(f(\vec{x}), y) = -y \log(f(\vec{x})) - (1 - y) \log(1 - f(\vec{x}))
\\
\text{Cost Function: } \quad
\begin{aligned}
& J(\mathbf{W}, \mathbf{B}) = \frac{1}{m} \sum_{i=1}^m L(f(\vec{x}), y), \\
& \mathbf{W} = [\mathbf{W}^{[1]}, \mathbf{W}^{[2]}, \mathbf{W}^{[3]}], \\
& \mathbf{B} = [\mathbf{\tilde{b}}^{[1]}, \mathbf{\tilde{b}}^{[2]}, \mathbf{\tilde{b}}^{[3]}].
\end{aligned}
$$

面已经介绍了损失函数的数学形式和代码。现在还有最后一点就是在迭代“训练”中，怎么求解代价函数的偏导。显然“训练”的过程就是最小化代价函数，比如使用“梯度下降”，那么每一次迭代都要计算代价函数对每一层每个神经元的每个参数的偏导。这工作量想想就惊人！更别说神经网络很难求出显式的偏导表达式。所以实际上，神经网络的“训练”使用“反向传播**(back propogation**)”来进行迭代，可以大大节省计算量。TensorFlow将上述“反向传播”寻找最低点的过程全部封装在model.fit()函数中，并迭代设定好的次数epochs

2 其他激活函数

2-1 Sigmoid激活函数的替代方案

前一直使用Sigmiod函数作为隐藏层和输出层所有神经元的激活函数。但Sigmoid函数显然也有其局限性

比如上面的“需求预测”问题，我们最开始假设隐藏层输出的有T恤的“心理预期价格”、“了解程度”、“产品质量”，但实际上这些指标并不一定都是二元的（为0-1之间的小数字），比如“认可度”可以有“不了解”、“一般了解”、“极度了解”、“完全传播开来”等。

于是我们不妨将“认可度”的范围扩展为到所有“非负数”，也就是从0到非常大的数字：ReLu函数（Rectified Linear Unit, 修正线性单元）：g(z) = max(0,z)

下面是三项常用的激活函数：

线性激活函数：g(z)=z, 人们也会称之为“没有使用任何激活函数”。
Sigmoid函数：$g(z) = \frac{1}{1 + e^{-x}}$ .
ReLU函数: g(z) = max(0,z)
Softmax函数：“第三节”讨论多分类问题时进行介绍

2-2 如何选择激活函数

那该如何选择激活函数呢？首先我们从输出层开始。输出层的激活函数通常取决于“目标值”，比如二元分类问题就使用Sigmoid函数、如果预测股票涨跌的回归问题就使用线性激活函数(因为有正有负)、如果是“预测房价”这样的回归问题就使用ReLU函数(因为房价非负)。而对于隐藏层来说，若无特殊原因，所有隐藏层的神经元都应选择ReLU函数。最早人们都默认使用Sigmoid函数，但是现在逐渐演变成默认使用ReLU函数，主要有以下几个原因：

ReLU函数形式更简单、计算更快。
ReLU仅在负数域平坦，而Sigmoid函数在正负两侧都平坦。而平坦的区域越大，会导致代价函数平坦的区域越大，“梯度下降”等算法训练模型的速度就越慢。

总结：“输出层”按照“目标值”取值范围选取，“隐藏层”默认全部采用ReLU函数(如下图)。

对于大多数情况、大多数应用来说，上述介绍的几个激活函数已经够用了。当然还有其他激活函数，比如Tanh函数、Leaky ReLU函数、Swish函数等。每隔几年，研究人员都会提出新的激活函数，这些激活函数在某些方面的性能确实会更好。想了解的话可以自行查阅。https://zhuanlan.zhihu.com/p/172254089

2-3 为什么需要激活函数

既然ReLU函数比Sigmoid函数计算更快，那能不能默认使用更简洁的“线性激活函数”呢？换句话说，能不能不使用激活函数呢？显然是不行的。由于“线性函数的线性组合还是线性函数”，若只使用线性激活函数，整个神经网络就会退化成“线性回归”。所以 尽量不在隐藏层使用线性激活函数。使用其他的非线性函数，比如ReLU函数，只要有足够多的神经元，通过调整参数就可以拟合出任意的曲线，进而实现神经网络想要的拟合效果。

我们举个简单的例子展示线性激活函数的局限性：

In general case:

使用线性激活函数的神经网络无法容纳比线性回归更复杂的模型

DeepSeek 对激活函数作用的总结

激活函数是神经网络中的核心组件之一，其作用可以概括为以下几个方面：

1. 引入非线性

核心作用：如果没有激活函数，神经网络的所有层都只是线性变换的叠加（相当于一个线性回归模型），无法解决非线性问题（如异或问题、图像分类等）。
示例：假设网络有两层线性变换 ( y = W_2(W_1x + b_1) + b_2 )，合并后仍为线性变换 ( y = (W_2W_1)x + (W_2b_1 + b_2) )，无法学习复杂模式。
激活函数的作用：通过非线性函数（如 ReLU、Sigmoid、Tanh）对每层的输出进行变换，使网络能够逼近任意复杂的函数。

2. 控制输出范围

根据任务需求调整输出：
- Sigmoid：将输出压缩到 ( (0,1) )，适用于二分类问题的概率输出。
- Tanh：输出范围为 ( (-1,1) )，适合需要中心化输出的场景。
- Softmax：多分类问题中，将输出转化为概率分布（和为1）。
- ReLU：输出范围为 ( [0, +\infty) )，适合隐藏层，保留特征的强度。

3. 梯度传递与训练稳定性

梯度消失/爆炸问题：
- Sigmoid 和 Tanh 的导数在输入较大时会趋近于零（梯度消失），导致深层网络难以训练。
- ReLU 及其变体（如 Leaky ReLU、ELU）在正区间的导数为1，缓解梯度消失问题，更适合深层网络。
死亡神经元问题：
- ReLU 在输入为负时梯度为零，可能导致部分神经元永久失效（可通过 Leaky ReLU 或参数化 ReLU 缓解）。

4. 稀疏性激活

ReLU 的稀疏性：当输入为负时，ReLU 输出零，使部分神经元处于非激活状态。这种稀疏性减少了参数依赖性，提升计算效率，同时可能增强模型的泛化能力（类似生物神经元的“选择性激活”）。

常见激活函数对比

激活函数	公式	优点	缺点	适用场景
Sigmoid	$ \frac{1}{1+e^{-x}} $	输出概率，平滑可导	梯度消失，非零均值	二分类输出层
Tanh	$ \frac{e^x - e^{-x}}{e^x + e^{-x}} $	零均值，输出范围更大	梯度消失	隐藏层或需要中心化输出
ReLU	$ \max(0, x) $	计算高效，缓解梯度消失	死亡神经元，负区间无响应	隐藏层（最常用）
Leaky ReLU	$ \max(\alpha x, x) $	缓解死亡神经元问题	需人工设置 ( \alpha )	深层网络隐藏层
Softmax	$ \frac{e^{x_i}}{\sum_j e^{x_j}} $	输出概率分布	仅用于多分类输出层	多分类输出层

选择激活函数的建议

隐藏层：优先使用 ReLU 或其变体（如 Leaky ReLU、Swish），计算高效且缓解梯度消失。
输出层：
- 二分类：Sigmoid。
- 多分类：Softmax。
- 回归任务：线性激活（无激活函数）或根据输出范围调整。
特殊场景：对梯度敏感的任务（如生成对抗网络）可尝试 Tanh。

总结

激活函数通过引入非线性、控制输出范围、调节梯度传递和增强稀疏性，使神经网络能够适应复杂的数据模式。其选择直接影响模型的训练速度、性能和泛化能力，需结合具体任务和网络结构权衡。

3 多分类问题 & Softmax

在第一节中，由于“手写数字识别”已经被我们简化成只识别数字1和数字0，所以使用了“二元交叉熵损失函数loss=BinaryCrossentropy()”，那如果要识别全部的数字0~数字9，又该如何设置损失函数呢？下面就来介绍。

3-1 多分类问题

显然，要识别全部的数字0~数字9，就需要将二元分类问题进行推广。于是，分类输出的目标值有多个可能的问题，便称为“多分类问题(multiclass classfication problem)”。比如“手写数字识别”要分类10个数字、“肿瘤检测”要分类多种恶化类型、流水线产品检测不同类型的缺陷等。

注：聚类是无监督学习，神经网络自行分类；多分类问题是有监督学习，只不过是类别多了。

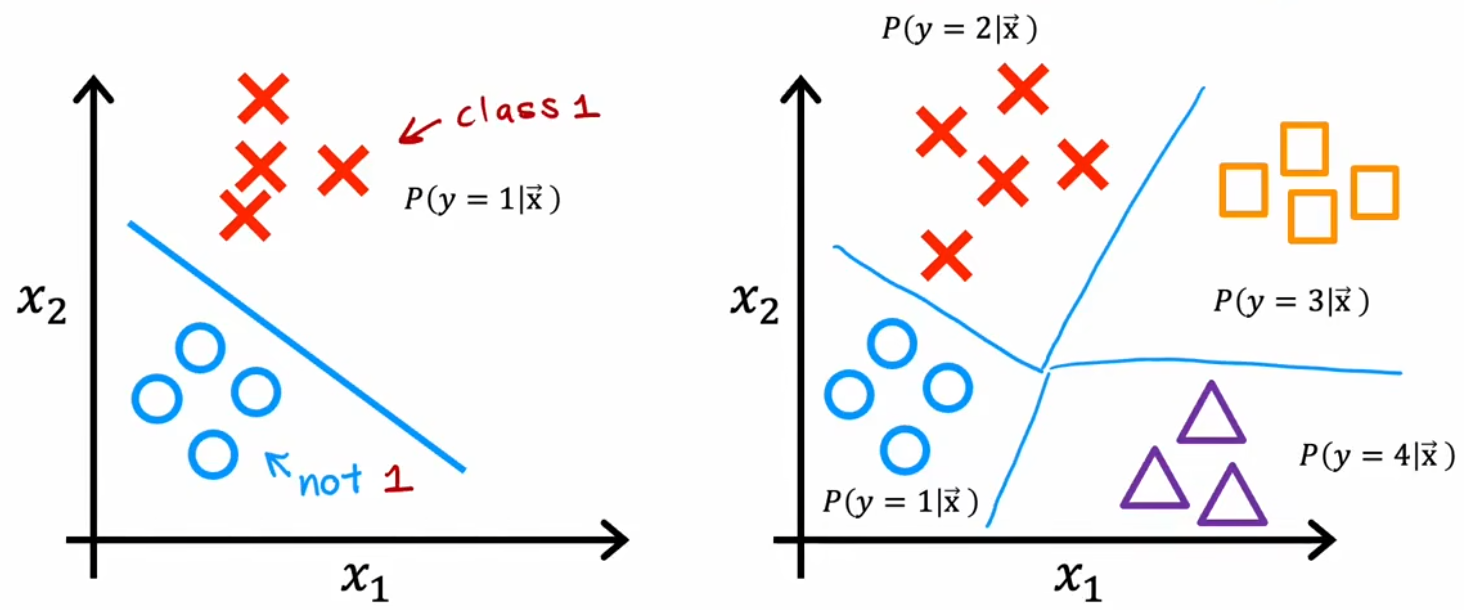
从二元分类推广到多分类

3-2 Softmax

下面是Softmax函数的定义，也就是 $g(z)$的定义：

j 为单层神经网络内的神经元索引；k 也为神经元索引，但其主要目的是将本层内所有神经元求和。
$a_j$：当前层第 j 个神经元的输出。

注1：尽管参数不完全一致，但 N = 2 时，“Softmax回归”会退化成“逻辑回归”。
注2：Softmax回归使用指数，不仅可以保证概率非负，同时也可以扩大不同值之间的差异。
注3：多分类问题所有可能输出的概率之和为1。

于是类似于“逻辑回归”的“二元交叉熵(Binary Crossen tropy)损失函数”，“Softmax回归”的损失函数为“稀疏分类交叉熵(Sparse Categorical Crossen tropy)”。同样也是，推理结果越接近真实结果，损失越小：

3-3 神经网络的softmax输出

显然，要创建解决多分类问题的神经网络，只需要更改输出层激活函数为“Softmax函数”、损失函数为“稀疏分类交叉熵”即可，代码如下：

注意到，Softmax层，也被称为“Softmax激活函数”，和之前的激活函数都不同。因为Softmax函数的输出$a_j$ 不只取决于当前的输入$z_j$, 而是取决于所有的输入$ z_1,…,z_N$, 所以Softmax层并不能逐个计算神经元的输出，而是需要“同时计算”该层所有神经元的输出。

3-4 softmax 的改进实现

虽然上述代码规定好了损失函数，但实际上并不采用上述代码。因为采用上面的代码，会要求TensorFlow保留损失函数计算的中间结果，$a_j, j = 1,…,N$。但实际上，多计算一个变量就会引入更多的舍入误差，尤其是“Sigmoid函数$\frac{1}{1+e^{-z}}$”, “Softmax函数$\frac{e^{z_j}}{\sum_{k=1}^{N} e^{z_k} }$ “ 的计算结果中，其总会有些值非常小，进而使得计算精度不足导致 舍入误差（IEEE754）. 为了消除这部分的舍入误差，我们可以令TensorFlow不要再计算中间结果$z$,而是直接将 $z$的表达式代入到损失函数中。这样TensorFlow会先化简损失函数表达式（重排列），再进行计算，从而减少一步的舍入误差：

如上图，现在我们仅使用线性激活函数，也就是最后一层仅计算z1~z10, 然后在损失函数处捕获整个损失计算，所以我们有了from_logits参数

使用数值稳定的数学公式（如Log-Sum-Exp技巧），避免中间步骤的数值问题。

分子分母同乘以max(z)可以减少e^x指数的大小，从而避免浮点数上溢或下溢

具体数学细节可看：课后资源: C2_W2_SoftMax 中的 Numerical Stability (optional)

总结

**何时使用线性激活 + from_logits=True**：当损失函数是交叉熵且需要数值稳定性和高效计算时。
何时保留Softmax激活：如果需要在模型推理时直接输出概率（例如，部署时），或使用不兼容from_logits的自定义损失函数。

3-5 多标签问题

最后，“多分类问题(multi-classfication problem)”和“多标签问题(multi-label problem)”非常容易混淆，本小节就是来区分一下这两个定义。“多标签分类”是一个输入，多个不同类型的分类。所以，“多标签问题”可以看成是多个“二元分类”的组合。比如下面的“多标签问题”就是由3个不同的“二元分类”组成的：

直观上，我们可能会想到针对不同的标签分类，创建各自独立的的神经网络，比如上图就创建三个独立的神经网络，但显然这看起来不聪明，所以实际上会创建一个神经网络同时解决这三个二元分类。创建网络时只要注意将最后的输出层调整为三个Sigmoid神经元即可。

下一节来介绍更加高级的神经网络概念，包括比“梯度下降”更好的迭代算法。

4 更加高级的神经网络概念

4-1 梯度下降法的改进：Adam算法

“梯度下降”广泛应用于机器学习算法中，如线性回归、逻辑回归、神经网络早期实现等，但是还有其他性能更好的最下滑代价函数的算法。比如“**Adam算法(Adaptive Moment estimation, 自适应矩估计)**”就可以自动调整“梯度下降”学习率 α 的大小，从而加快“梯度下降”的收敛速度。下面是其算法逻辑和代码示例

“Adam算法”并不只使用同一个学习率α，而是 针对每个参数都定义一个 $\alpha_j$
如果参数一直向同一个方向前进，就逐步增大该参数的学习率；若每次方向都不一样(振荡)，就逐步减小学习率。
Adam算法”还需要一个参数来控制每个参数的学习率的增大或减小的速度——全局学习率(下面设置为$10^{-3}$ )

4-2 其他的网络层模型

目前为止学习到的所有神经网络都是“**密集层类型(dense layer type)”，也就是层内的每一个神经元都会得到上一层的所有输入特征。虽然“密集层类型”的神经网络功能很强大，但是其计算量很大。于是，Yann LeCun 最早提出“卷积层(convolution layer)**”，并将其应用到计算机视觉领域。“卷积层”中，每个神经元只关心输入图像的某个区域。如下左图中，对于输入图像，每个神经元只关心某个小区域(按照颜色对应)。“卷积层”的优点如下：

加快计算。
需要的训练集可以更小，并且也不容易“过拟合”。（Week3会更加详细的介绍“过拟合”）

上图给出了“心电图监测”问题：根据心电图(electrocardiogram, EKG/ECG)判断是否有心脏病。

输入特征：长度为100的心电图信号。

输出：有心脏病的概率。

上右图便给出了“心电图监测”问题(本小节开始的说明)的卷积神经网络示意图，每个神经元只能查看一个小窗口（如第一个神经元查看x1-x20）;下一层也可以是一个卷积层，第1个单元只会查看$a_1^{[1]}到a_5^{[1]}$,第2个单元只会查看$a_3^{[1]}到a_7^{[1]}$, 第3个单元只会查看$a_5^{[1]}到a_9^{[1]}$, 然后将第二层$a^{[2]}$ 输入到sigmoid单元，以便对是否存在心脏病进行二元分类。

显然，改变每个神经元查看的窗口大小，每一个有多少神经元，有效的选择这些参数，可以构建比“密集层类型”更加有效的神经网络。

除了“卷积层”之外，当然还有其他的神经网络层类型，将不同类型的“层”结合在一起，组成更加强大的神经网络：

全连接层（Fully Connected Layer）：全连接层是最简单的神经网络层，其中每个神经元与上一层的所有神经元相连接。

卷积层（Convolutional Layer）：卷积层用于处理图像和其他二维数据，通过卷积操作提取图像的局部特征。

池化层（Pooling Layer）：池化层通常与卷积层结合使用，用于减小特征图的空间尺寸，提高计算效率，并减少参数量。

循环神经网络层（Recurrent Neural Network Layer）：RNN层用于处理序列数据，具有记忆性，能够捕捉时间上的依赖关系。

长短时记忆网络层（Long Short-Term Memory Layer，LSTM）：LSTM是一种特殊的循环神经网络层，具有更强大的记忆性，适用于处理长序列依赖关系。

……

5 反向传播

“反向传播”是“自动微分(auto-diff)算法”的一种。接下来介绍TensorFlow如何使用“反向传播”，计算神经网络的代价函数对所有参数的偏导。

5-1 计算图和导数

显然，由于神经网络可以创建的相当庞大，所以很难显式的写出偏导表达式。此时，我们求解代价函数偏导的思路就转成，求解代价函数在该点切线的斜率，也就是使用很小的步长来近似当前点的切线斜率。但是神经网络通常又有很多层，于是对于每个神经元的每个参数都通过这种方式，直接迭代一次神经网络求解对一个参数的偏导，显然也不现实。于是，我们先通过“计算图(Computation Graph)”来研究一下神经网络的计算流程，找找灵感，比如下面对于单神经元网络的代价函数计算：

也就是，将整体的计算过程拆成一步一步的，就组成了“计算图”。从左到右，求解当前点的代价函数大小很简单。但注意到，如果我们想要求解代价函数的表达式时，还可以根据上述“计算图”写出求导的“链式法则(chain rule)”！！而且“链式法则”的顺序正好是从右向左的！！由于越靠右的节点也会被更多的参数共用，于是反向传播一次，便可以把依次把路径上的每一个参数的偏导都求解出来。而不是针对每个参数，都额外增加一点，通过从左到右计算代价函数的变化率来求得相应参数的偏导。于是，若“计算图”总共有 N 个节点、P 个输入参数，要计算所有函数偏导：

反向传播：只需大约 N + P 个步骤。

针对每个参数求切线斜率：大约 N × P 个步骤。

总结：在“计算图”中使用“链式法则”可以大大加快神经网络的训练速度！！
反向传播就是从左到右计算代价函数，然后从右向左计算所有参数的偏导。

5-2 大型神经网络案例

在关于反向传播的最后一节中，让我们来看一下如何将反向传播的思想应用到大型神经网络中。

先“前向传播”计算神经网络中所有神经元的取值，然后一次“反向传播”遍历走完所有节点，即可计算出神经网络的代价函数对每个神经元的每个参数的偏导。显然，此时“计算图”实际上就相当于神经网络。

在许多年前，在Tensorflow和pytorch等框架兴起之前，研究人员过去必须手动使用微积分计算他们想到训练的神经网络的导数，因此在现代程序框架中，你可以指定一个forward prop 并让他为你处理back prop; 很多年以前，研究人员手写神经网络，手动使用微积分计算导数，然后神经网络执行他们在纸上费力推导出来的一堆方程，以实现反向传播，多亏了计算图和这些进行导数计算的技术，如autodiff, 用于自动微分，这种研究人员手动使用微积分求导的过程is no longer done. 所以随着神经网络的成熟，这些工作量下降了，这对很多人来说是令人鼓舞的。

6 Exercise：多分类的神经网络手写数字识别

可以在课程资料中的C2_W2_Assignment中进行练习

# 导入头文件
import numpy as np
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.activations import linear, relu, sigmoid
import matplotlib.pyplot as plt

plt.style.use('./deeplearning.mplstyle')
import logging

logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)

# 加载训练集：5000张手写体图片，每张图片大小20x20
X = np.load("data/X.npy")  # 5000x400
y = np.load("data/y.npy")  # 5000x1

# 定义神经网络
model = Sequential(
    [
        tf.keras.Input(shape=(400,)),  # 输入特征的长度
        Dense(units=25, activation='relu', name='layer1'),
        Dense(units=15, activation='relu', name='layer2'),
        Dense(units=10, activation='linear', name='layer3'),
    ], name="my_model"
)

# 编译模型
model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(learning_rate=0.001)
)

# 训练模型
history = model.fit(X, y, epochs=40)

# 预测结果
image_new = X[1015]
prediction = model.predict(image_new.reshape(1, 400))  # prediction
yhat = np.argmax(prediction)
prediction_p = tf.nn.softmax(prediction)
print(f" Largest Prediction index: {yhat}")
print(f"The Probability of Largest index: {prediction_p[0, yhat]:0.2f}")