机器学习吴恩达笔记 week3
1 逻辑回归
1-1 动机与目的:线性回归不适用于分类问题
概念明晰:
本课程中,class/category两者都表示“分类问题”的输出类别,两者意义相同。 “逻辑回归(logistic regression)算法”用来解决“分类问题(classfication)”。这是历史遗留的命名问题。
本周将学习“分类问题”,其输出为有限取值,而不是某段范围内无限的数字。若分类问题的输出结果只有两种可能的分类/类别(class/category),就被称为“二元分类(binary classfication)”,比如下面的三个问题:
是否为垃圾邮件?(0/1) 是否为交易欺诈?(0/1) 是否为恶性肿瘤?(0/1)下图与Week1“肿瘤分类”示意图的不同,仅在于下图画出了实际的纵轴。 惯例:0表示“否”,1表示“是”。0/1 只有 否定/肯定 含义,并不具有褒贬含义。
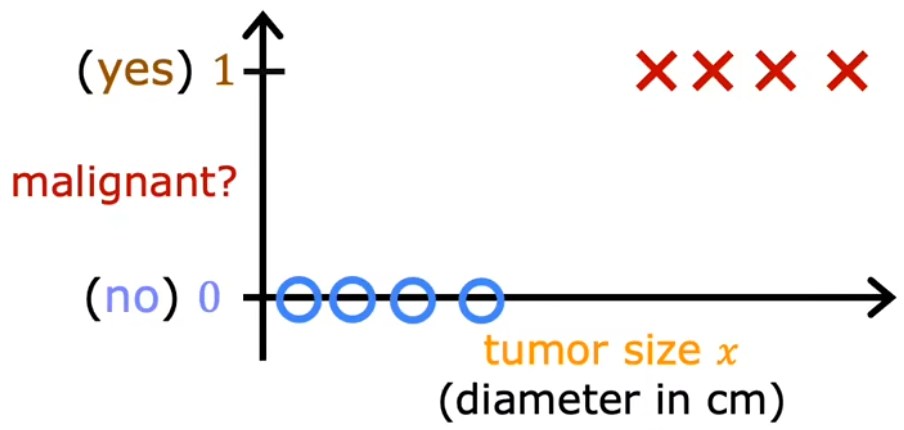
若我们采用前面学过的“线性回归”,对于特定的训练集(没有最右侧样本),看起来是合理的。因为此时以0.5作为阈值,其与样本拟合线(蓝色)相交在横轴上的点,便可以作为一个边界(蓝色),边界左侧都是良性(0),边界右侧都是恶性(1)。但此时额外添加一个最右侧的样本,显然拟合线(绿色)和横轴上的边界(绿色)都和预期不符:
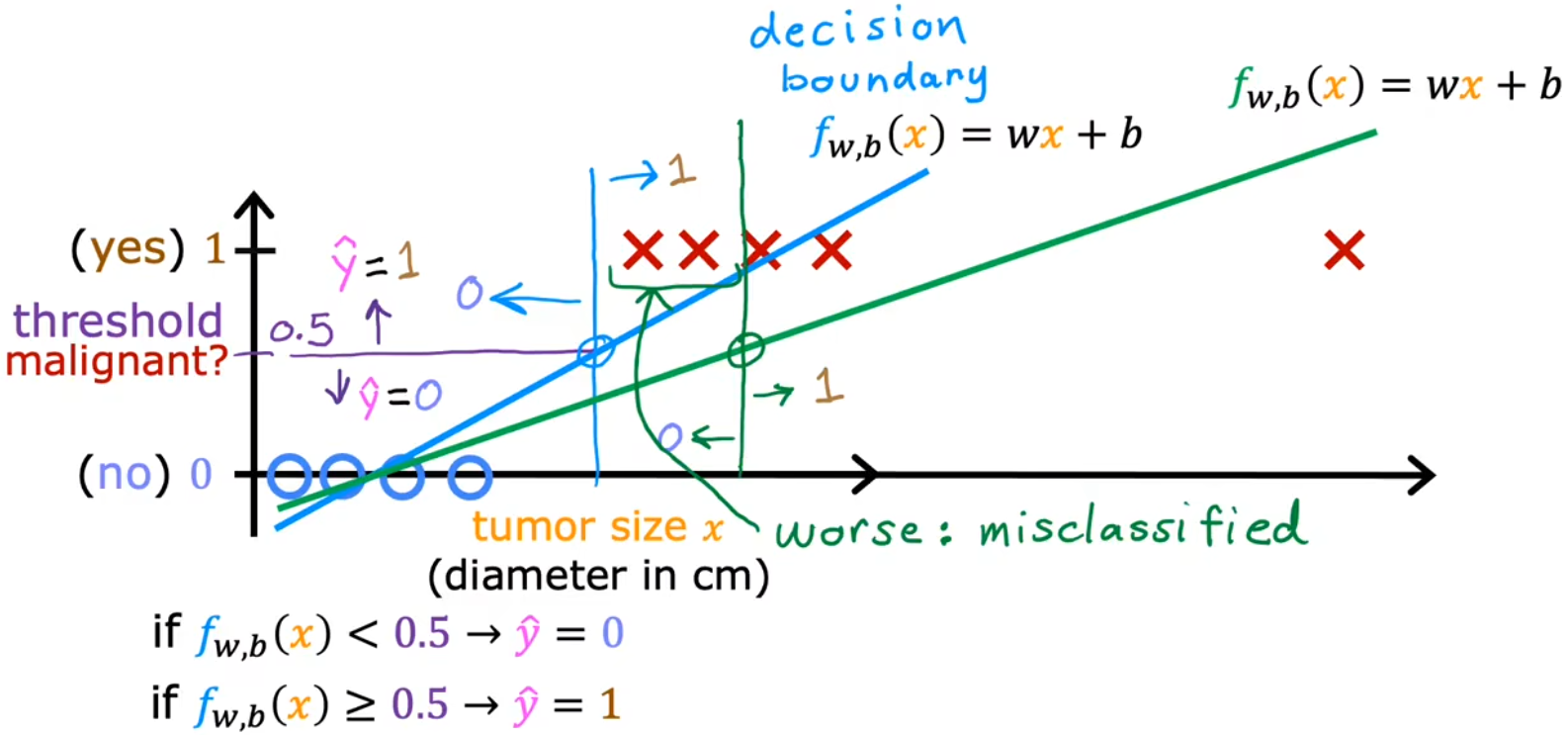
- 决策边界(decision boundary):横轴上的边界。
总的来说,有时候可以很幸运地使用“线性回归”解决“分类问题”,但大多数情况下都不行,线性拟合不适用于分类问题。于是下面将介绍“逻辑回归(logistic regression)”,来解决分类问题,这也是一种当今被广泛使用的算法。
1-2 逻辑回归模型
“逻辑回归”是一种当今被广泛使用的算法,比如生活中的“精准广告投放”算法,老师说他在工作中也经常用。“逻辑回归(logistic regression)”使用S型曲线来进行函数拟合,最常见的S型曲线就是 Sigmoid function,其也被称为 logistic function:
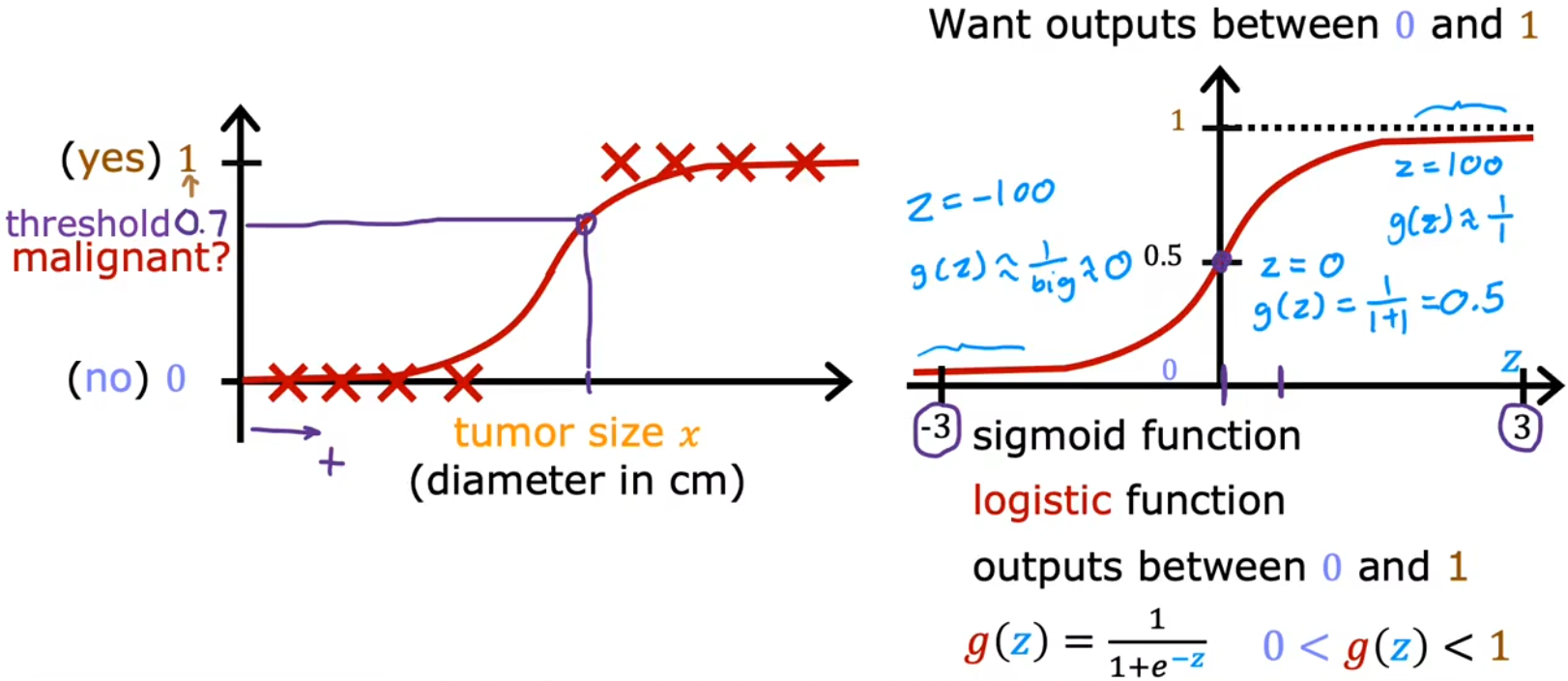
只要根据样本的散点图,选择不同的方式对 $z$ 拟合(见下一小节),就可以解决各种各样的分类问题。比如在“肿瘤分类问题”中,令 $z = \vec{x} \cdot \vec{w} + b$ , 并将其代入到igmoid函数中,便可得到“(多元)逻辑回归算法”的数学模型: $$ f_{\vec{w},b}(\vec x) = g(z) = g(\vec{w} \cdot \vec{x} + b) = \frac{1}{1+e^{-(\vec{w} \cdot \vec{x} + b)}} $$ 对于使用Sigmoid函数构建的“逻辑回归”的数学模型来说,输入相应的特征或特征集,就会输出一个0~1之间的数字,这个输出可以认为是 y = 1 的“概率(probability)”:$f_{\vec{w},b}(\vec x) = \mathrm{P}( y=1 \mid \vec{x},\vec{w},b)$
也就是,在给定参数 $\vec{w}$ 和 $\vec{b}$、输入 $\vec{x}$ 的情况下,其输出 $y = 1$的概率。比如对于上述“肿瘤分类问题”来说,输出的数字就表示“为恶性肿瘤的概率 P ( 1 ) ”,若输出0.7,则表示该模型认为有70%的可能是恶性肿瘤(30%的可能不是恶性肿瘤)。
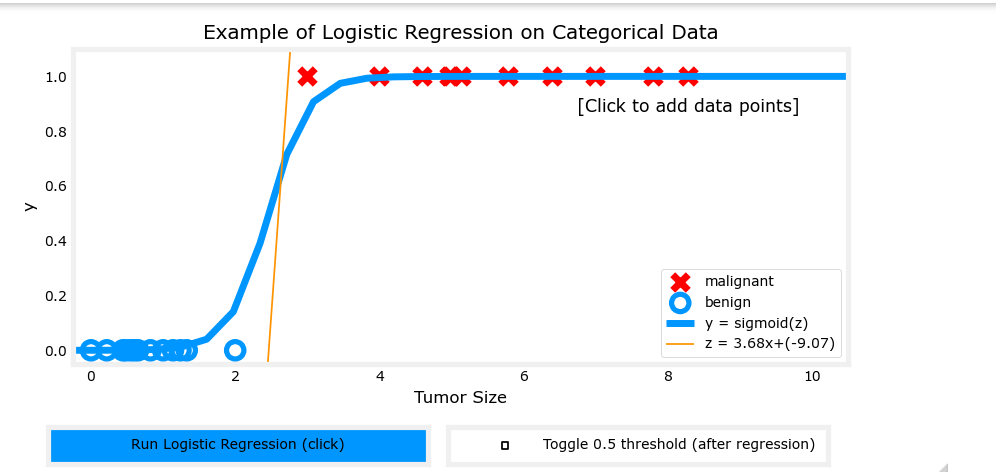
1-3 决策边界
前面提到,“逻辑回归”的输出表示“输出为1的概率”。那么很自然的便想到,我们应当选取一个“阈值”,当输出概率大于这个“阈值”时,就可以认为输出结果为1,这个“阈值”就是“决策边界(decision boundary)”。显然,最直观的决策边界就是选取 $g(z) = 0.5$,也就是:
$$ f_{\vec{w},b}(\vec x) = g(z) \geq 0.5 \Rightarrow \hat{y} = 1 \ f_{\vec{w},b}(\vec x) = g(z) < 0.5 \Rightarrow \hat{y} = 0 $$ 而决策边界的形状是由 $z$ 决定,令 $z = \vec{w} \cdot \vec{x} + b$ ,决策边界便为一条直线;令$z$ 为更高阶的多项式,则可以得到形状更复杂的决策边界,这便是“逻辑回归”可以学习相当复杂的数据集的奥妙所在。下面是两个示例:
示例1:决策边界为直线
令$z = w_0x_0+w_1x_1 + b$: 假设$w_1 = 1,w_2=1,b=-3$ ,决策边界g(z) = 0.5 于是经过移项可得到决策边界为$x_1 + x_2 = 3$
(下图紫色直线),决策边界的下方认为是0、上方认为是1,符合直观
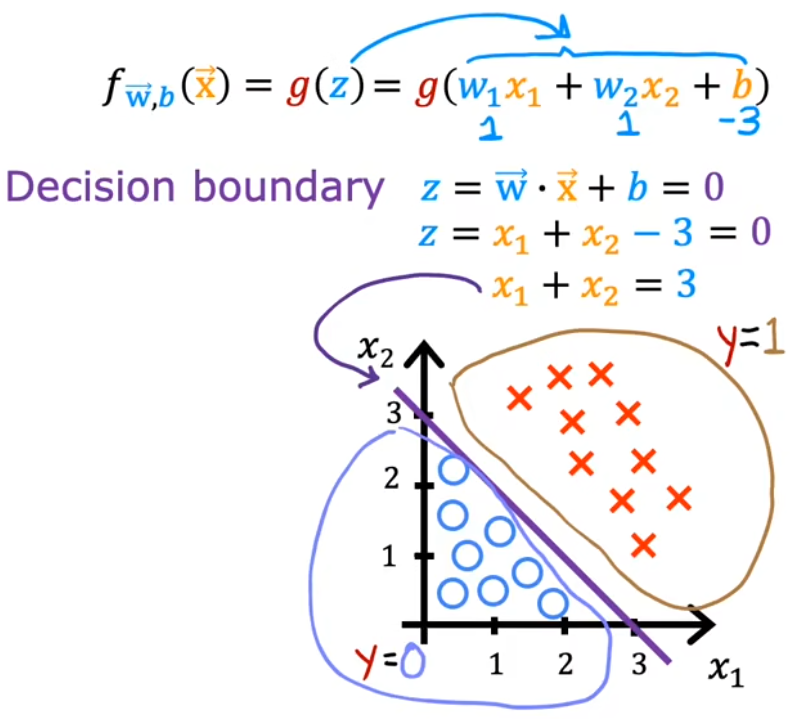
$x_1,x_2$ 表示两种输入特征,红叉表示正向示例(1),蓝圈表示反向示例(0)。
示例2:决策边界为圆

2 逻辑回归的代价函数
概念明晰:
- 本节中,单个样本使用“损失(loss)函数”,整个训练集使用“代价(cost)函数”。“代价”是所有样本“损失”的平均值。
- 本课程中,若无特殊说明,$log(\cdot)$函数都默认对自然函数e 取对数,即$log(\cdot)=log_e(\cdot)=ln(\cdot)$
和“线性回归”类似,给定“逻辑回归”的模型后,也要讨论一下“逻辑回归”的“代价函数”,用来衡量当前参数对于训练集的匹配程度。在“线性回归”中,我们使用“平方误差”来计算模型的代价函数,但对于“逻辑回归”问题来说,若也采用平方误差函数,那么它的代价函数就如同下图所示,是一个非凸函数,任意一个局部极小值都可能让梯度下降法收敛。显然,“平方误差”不能作为“逻辑回归”的代价函数: 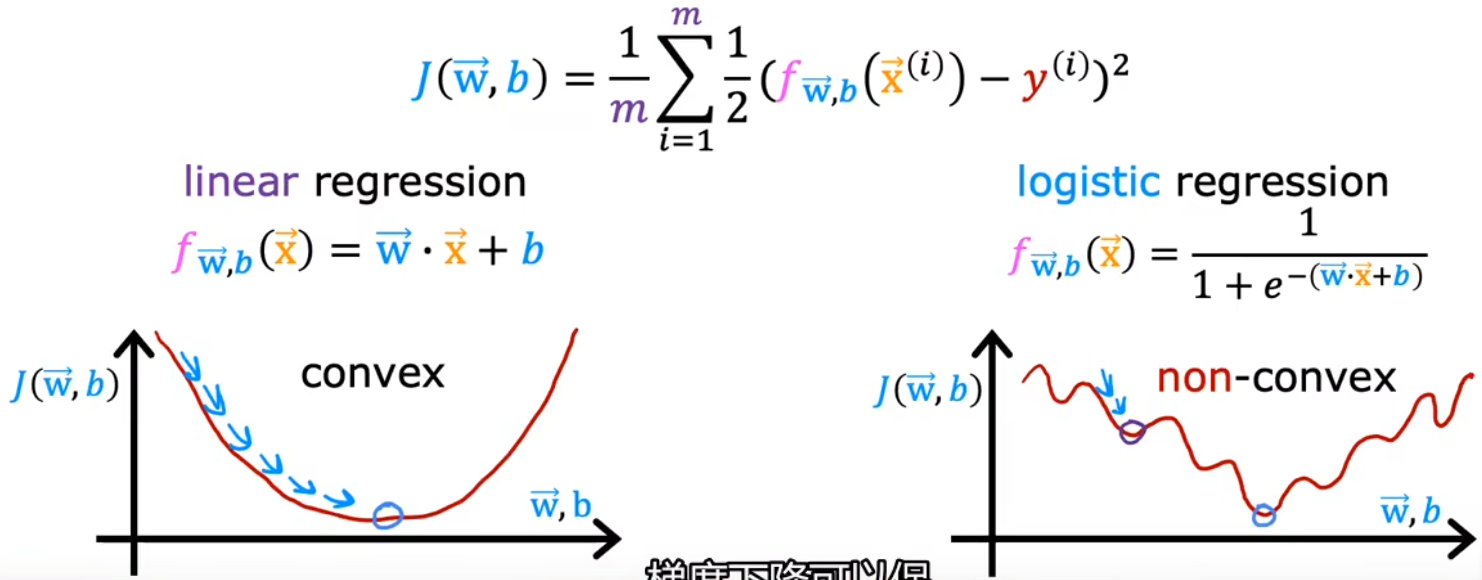
于是定义下面这种形式的 负对数形式的损失函数 $L( f_{\vec{w},b} (\vec{x}^{(i)}) , y^{(i)} )$ , 进而保证代价函数$J(\vec{w},b)$在逻辑回归中为凸函数,进而在后续可以使用梯度下降法。 $$ Logistic \ loss \ function: L( f_{\vec{w},b} (\vec{x}^{(i)}) , y^{(i)} ) = \left{\begin{matrix} -log(f_{\vec{w},b} (\vec{x}^{(i)})), \ y^{(i)} = 1 \ \ -log(1- f_{\vec{w},b} (\vec{x}^{(i)}) ), \ y^{(i)} = 0 \end{matrix}\right. $$
$L( f_{\vec{x},b} (\vec{x}^{(i)}) , y^{(i)} )$: 损失函数,表示单个训练样本 $(\vec{x}^{(i)},y^{(i)})$ 的损失,在“线性回归”中,损失函数为 $\frac{1}{2} (f_{\vec w,b}(\vec x^{(i)}) - y^{(i)})^2 $
而在逻辑回归中 , 损失函数如上面的公式所示
预测模型$0<f_{\vec w,b}(\vec x^{(i)}) < 1$
可知逻辑回归代价函数(cost function)如下所示 $$ logistic \ cost \ function = J(\vec w,b) = \frac{1}{m} \sum_{i=1}^{m} L( f_{\vec w,b} (\vec{x}^{(i)}) , y^{(i)} ) $$
当训练数据 $y^{(i)} = 1$时,如下图,预测值$f_{\vec w,b}(\vec x^{(i)})$ 越接近1,损失值越小甚至趋于0;越远离1,损失函数越大,并且损失的增长速度越来越快,甚至趋于无穷$∞$
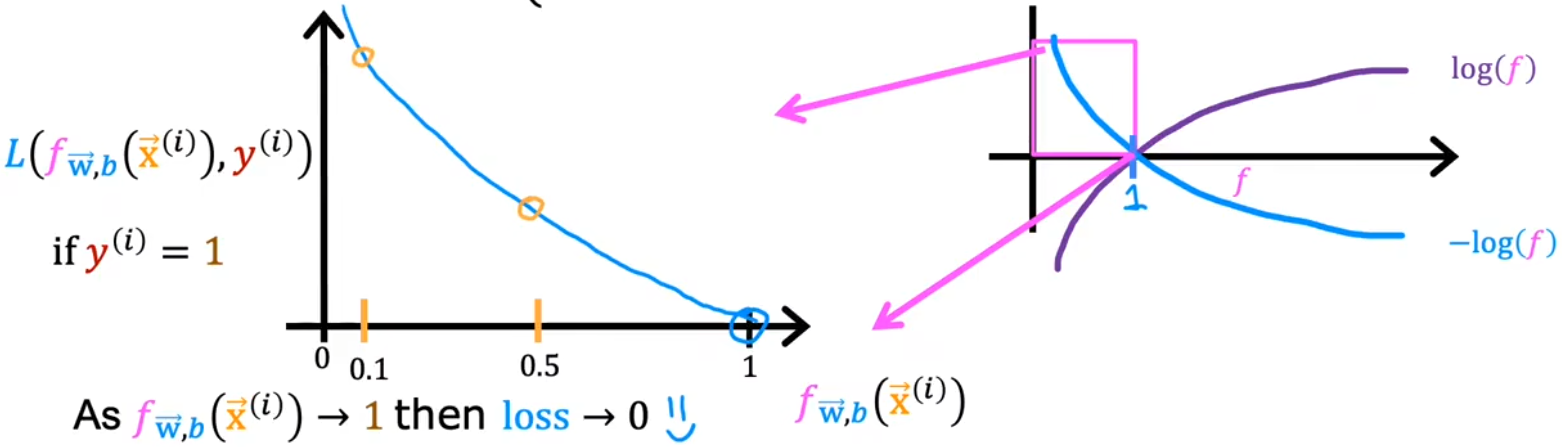
当训练数据 $y^{(i)} = 0$时,如下图,预测值$f_{\vec w,b}(\vec x^{(i)})$ 越接近0,损失值越小甚至趋于0;越远离0,损失函数越大,并且损失的增长速度越来越快,甚至趋于无穷$∞$
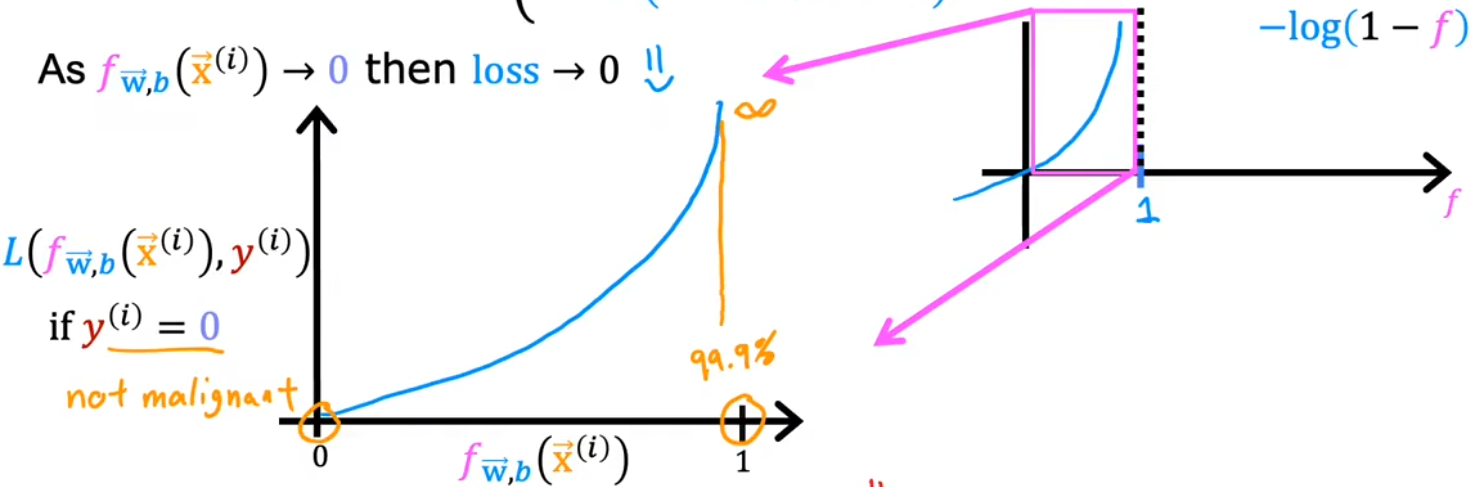
简化逻辑回归代价函数


上述“代价函数”使用了统计学中“最大似然估计(maximum likehood estimation)”的原理。这只是个特定的代价函数,当然还有其他无数种代价函数。
3 实现梯度下降
于是,对上一节给出的“代价函数”进行梯度下降,我们便可以完成整个“逻辑回归”,进而找到最合适的参数$ \vec{w}$和$b$。注意,“逻辑回归”中梯度下降法的表达式仍然和“线性回归”一样(计算上的巧合):

推导过程如下: 
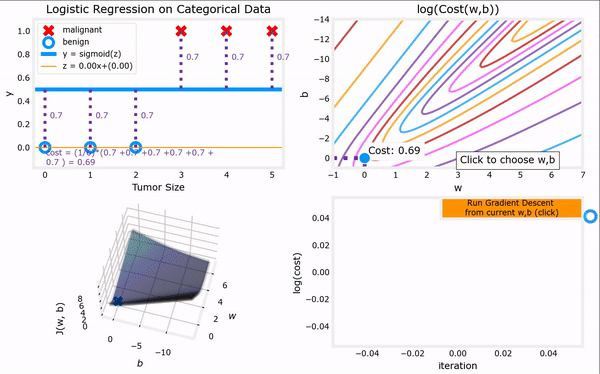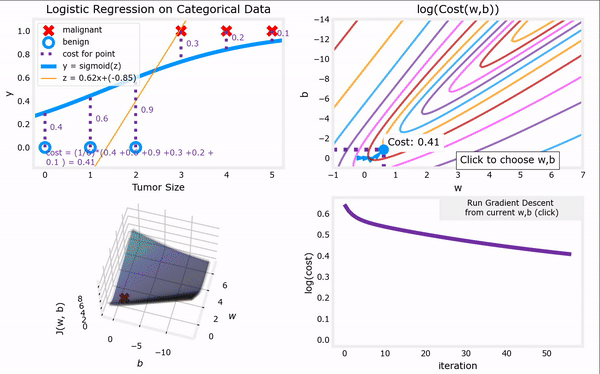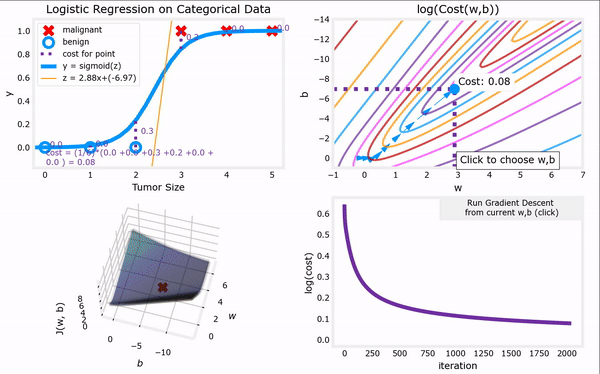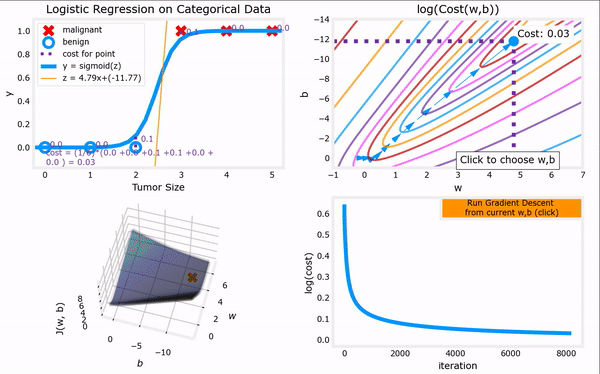
逻辑回归的梯度下降过程:代码见吴恩达机器学习课程资料:C1_W3_Lab06_Gradient_Descent_Soln
4 过拟合和正则化
4-1 过拟合
现在已经学完“线性回归”和“逻辑回归”了,并且也介绍了“_学习曲线_”、“_向量化_”、“_特征缩放_”等一系列加速算法的方法。但是当梯度下降法迭代完成后,还有一类特殊的情况没有介绍,那就是“**过拟合(overfitting)”和“欠拟合(underfitting)”。本节将介绍这两个概念,并介绍解决这类问题的方法——“正则化(regularization)**”。
注:“Underfit”和“High bias”都表示欠拟合;“Overfit”和“High variance”都表示过拟合。
下面给出了“房价预测”、“肿瘤分类”两种问题中的“过拟合/欠拟合”情况
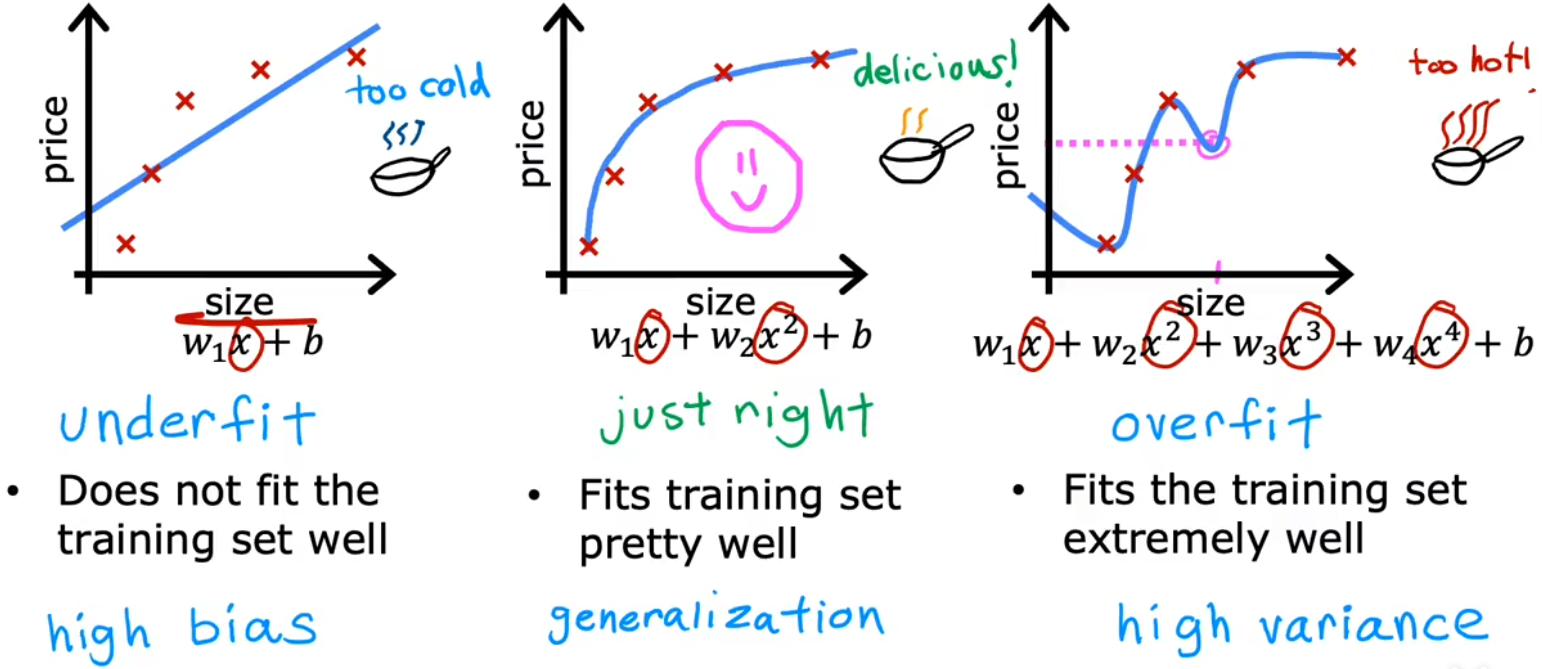
图源:吴恩达机器学习课程 https://www.coursera.org/specializations/machine-learning-introduction
- 欠拟合/高偏差:特征太少,甚至都不能很好的拟合训练集。“高偏差”有两层含义,一方面是拟合线和训练集的偏差很大;另一方面是因为我们先入为主的使用直线拟合,这本身与实际情况就是一种很大的偏差。
- just right:恰到好处!没有特别的术语描述这种情况。但即使对于一个全新的输入,也可以给出恰当的输出,于是称这样的模型具有很好的“泛化(generazilization)”特性。
- 过拟合/高方差:有太多的特征,可以完美的拟合数据集。但对于全新的输入,并不能给出恰当的输出。甚至训练集稍微变化一点点,都会拟合出完全不一样的曲线,也就是“高方差”。
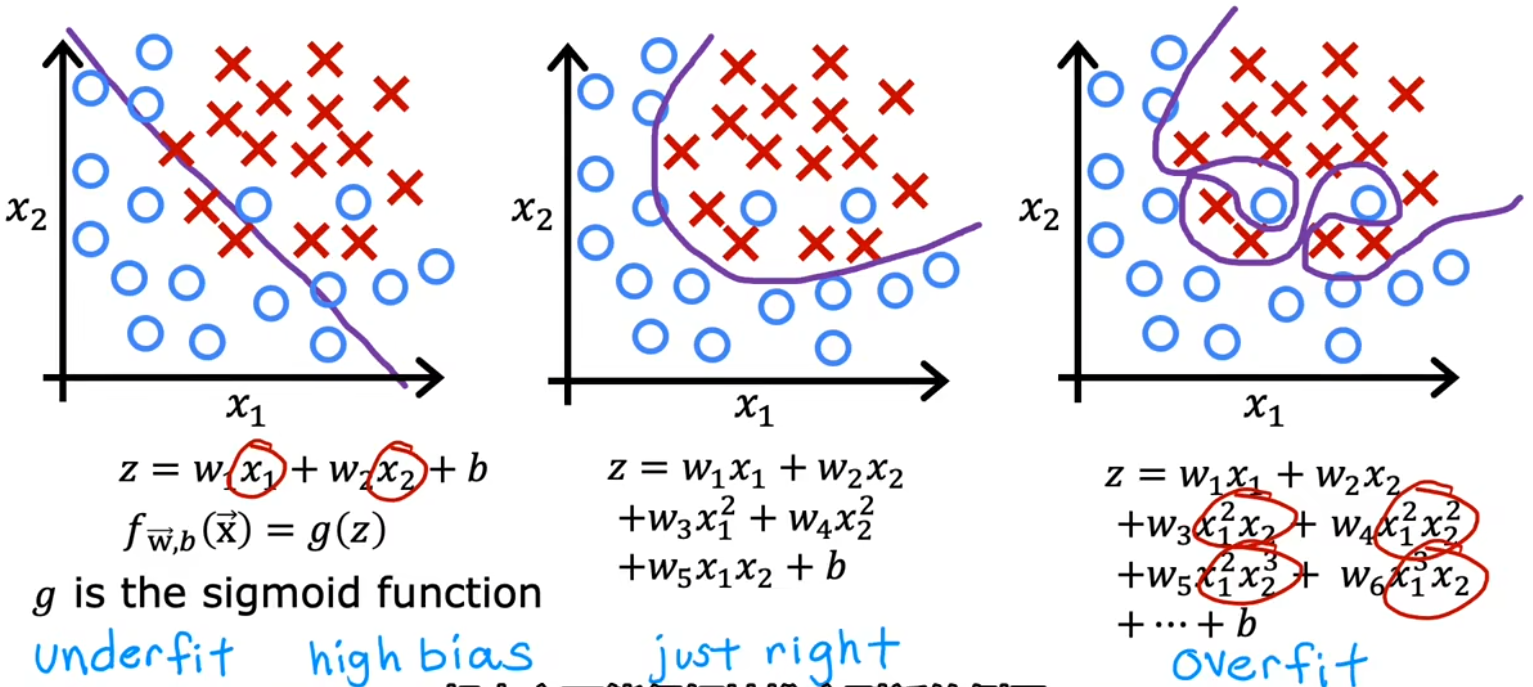
- 欠拟合/高偏差:决策边界是一条直线,看起来还行,但显然没有很好的学习到训练集。
- just right:决策边界是椭圆或椭圆的一部分,较好的拟合了数据,虽然并不是完美符合所有的训练数据。
- 过拟合/高方差:决策边界非常扭曲,以图完美符合所有的训练数据,但显然并不具有泛化特性。
4-2 解决过拟合
现在先只介绍如何解决过拟合,后续课程会介绍如何避免算法出错,并且介绍用于识别 欠拟合/过拟合 的工具
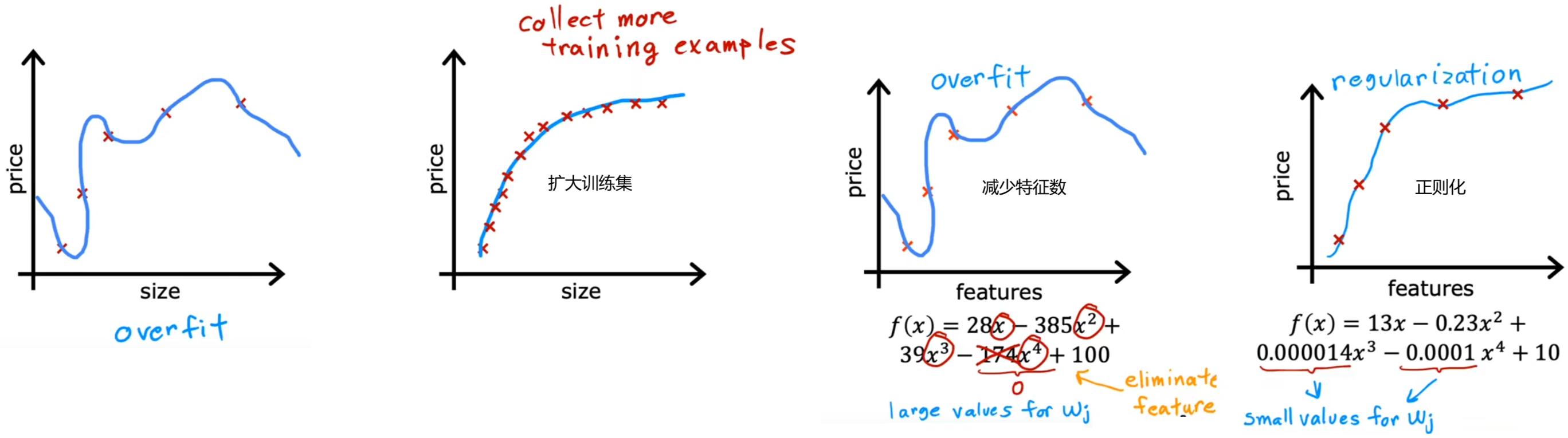
- 扩大训练集:此时即使有很多特征,相比于训练集很小时,其拟合曲线也会相对平滑。缺点是不一定能获取更多的训练数据。 减少特征数:也称为“特征选择”。“特征选择”除了靠直觉,在Course2中也会介绍一种自动选择特征的方法。缺点是有可能会丢弃有用特征。
- 减少特征数:也称为“特征选择”,选择出你认为最相关的一组特征,缺点是有可能会丢弃有用特征 。“特征选择”除了靠直觉,在Course2中也会介绍一种自动选择特征的方法。
- **正则化(regularization)**:保留所有的特征,但对于某个很大的特征(幂次很高)x_j,减小其参数w_j(通常不会调整参数b),这是一项非常有用的技术,可以用于训练学习算法,特别是神经网络。
注意:新版本sklearn如果出现type error 参数错误和需要修改下面的plt_overfit代码,
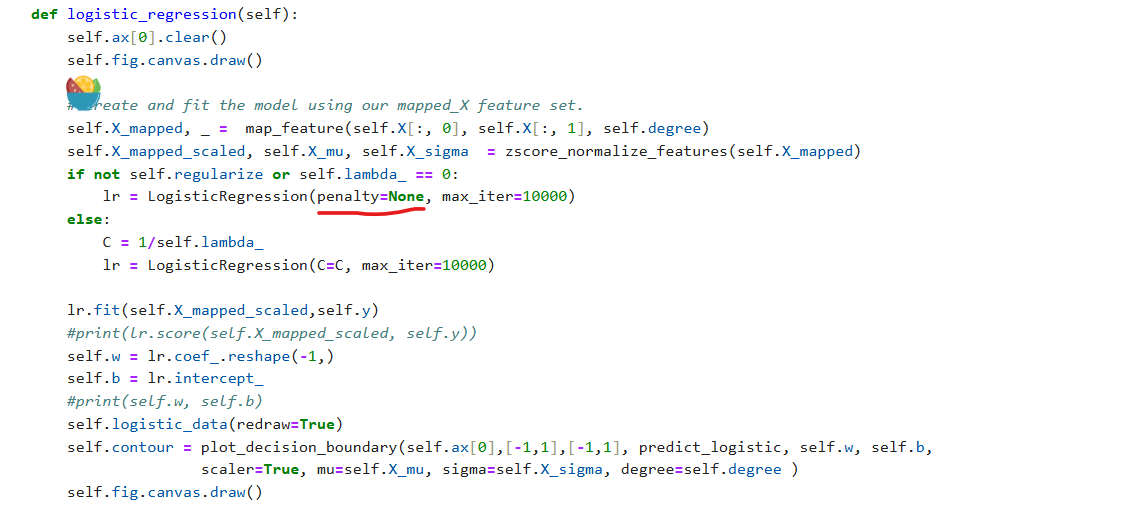
参数penalty是python None而不是字符串’none’,

normalize 参数已经在新版本被移除
4-3 正则化
本节将具体介绍如何进行“正则化”。将会改进代价函数,来将其应用于“正则化”的本质就是改进代价函数,添加新的“**正则项(regularization term)**”,用于控制参数的大小: $$ Modified \ cost \ fuction: \min_{\vec w,b} J(\vec w,b)= \underbrace{\frac{1}{m} \sum_{i=1}^{m}L(f_{\vec w,b}(\vec x^{(i)}),y^{(i)})}{\text{orginal cost}} \ + \ \underbrace{\frac{\lambda}{2m} \sum_{i=1}^{m} w_j^2 }{\text{regularization term}}
- \underbrace{\frac{\lambda}{2m} \sum_{i=1}^{m}b^2}_{\text{no use}} $$
$\lambda$: 正则化参数(regularization parameter); λ=0时,没有正则化,此时模型会尽可能完美拟合数据(也可能会过拟合);随着$\lambda$增大,所有的$w_j$都会减少, 但 $\lambda$ 过大时,曲线会过于平滑,就会“欠拟合”。所以 $ \lambda $ 算是在平衡 “数据拟合” 和 “曲线平滑” 这两个目标。
$\frac{\lambda}{2m} \sum_{i=1}^{m} w_j^2$ : 正则项(regularization term)。分母中的 “m” 是为了消除样本个数对于正则化效果的影响,而由于参数是平方项,分母中的 “2 ” 则是为了使代价函数偏导更加简洁。
$\frac{\lambda}{2m} \sum_{i=1}^{m}b^2$ : 有些工程师会在代价函数后加上对参数 b 的惩罚项,但实际上并不会有什么帮助。
可见“正则化”主要用于 解决“过拟合”,其作用是 使 所有 参数 同时 增大或减小,但不同参数的变化速度不同。相比于范围较小的特征,“正则化”对于范围较大的特征的参数影响更大,也就起到了调节曲线平滑程度的作用。
4-4 用于线性回归的正则化方法
$Linear \ regression \ model: f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b$
$Linear \ cost \ function: J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2$
梯度下降
$$\begin{align_} &\text{repeat until convergence:} \; \lbrace \ & \; \; \;w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1} \; & \text{for j := 0..n-1} \ & \; \; \; \; \;b = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \ &\rbrace update \ simultaneous \end{align_}$$
$$\begin{align_} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} + \frac{\lambda}{m} w_j \tag{2} \ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3} \end{align_}$$
综上
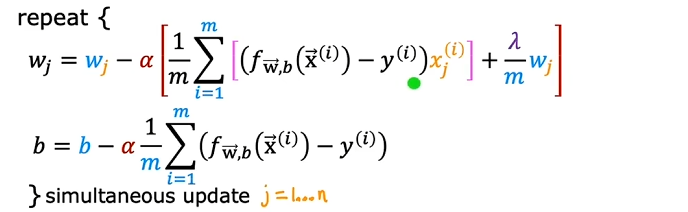
下面来进一步分析参数的更新过程(同样也适用于“逻辑回归”中的正则方法):
$$ w_j = w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m} \left[ (f_{\tilde{w}, b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) $$
$$ = \underbrace{\left(1 - \alpha \frac{\lambda}{m}\right) w_j}{\text{shrink } w_j} - \underbrace{\frac{\alpha}{m} \sum{i=1}^{m} \left[ (f_{\tilde{w}, b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right]}_{\text{usual update}} $$
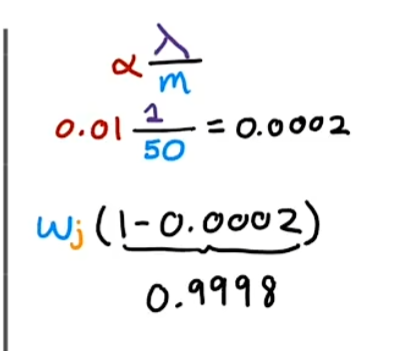
第一项:添加正则化后,会在每次迭代过程中,都使参数 $w_j$乘以一个略小于1的常数。
第二项:对于非正则化线性回归,正常的梯度下降法更新过程。
4-5 用于逻辑回归的正则化方法
我们在先前的课程中学到逻辑回归的代价函数如下 :
$$ J(\mathbf{w},b) = \frac{1}{m}\sum_{i=0}^{m-1} \left[ (-y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right)\right] $$
在这里逻辑回归模型:
$$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = sigmoid(\mathbf{w} \cdot \mathbf{x}^{(i)} + b) \tag{4} $$
因此,对于正则化的逻辑回归: $$J(\mathbf{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ -y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \right] + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2 \tag{3}$$
梯度下降和上节高度相似:




